Trajectory Forecasting Using Segmentation & Attention

Asish Gumparthi, Luis Figueroa, and Dhruv Vashisht | Course Project, Visual Learning and Recognition, Spring 2021

Code | Video

Project Website: https://trajectory-prediction.figueroaluis.com/

Figure 1. Qualitative human trajectory predictions from our framework. Yellow is ground truth and Pink is model predictions.

Motivation and Task

Trajectory Prediction is the problem of predicting the short-term and long-term spatial coordinates of various road-agents such as cars, buses, pedestrians etc. Accurate and robust trajectory prediction is critical for the advancement of autonomous vehicles as it allows for better maneuverability in dense urban environments. As such, modeling pedestrian motion is non-trivial, as human motion paths are affected by environmental factors, leading to many plausible ways by which people could move. These movements vary, especially in complicated scenes where pedestrians move around obstacles such as trees, garbage bins, or benches. In addition, occlusion presents an additional challenge when tracking pedestrians. In this project, we wish to explore the use of segmentation information, in addition to a subject's movement and social interactions, to improve the trajectory prediction of pedestrians. Semantic segmentation can provide us with contextual information which can be used as a constraint to predict movements that are physically possible. This can further be expanded to include only socially acceptable movements, e.g. movements are allowed on a sidewalk and not on top of a car. Furthermore, we introduce the use of attention mechanisms on pedestrian movements as additional information to predict their future trajectory.

For this project, the task of trajectory prediction is defined as follows:
Given a scene with multiple human subjects, we observe the spatial coordinates of the person of interest for the first 5 steps and then predict their trajectory for the next 5 steps, that is 2 seconds into the future.
We formally define the problem as follows, given spatial coordinates (xt ; yt) over a period t = 1, 2, ..., t of each pedestrian's trajectory in a video as input, the goal is to predict the future location (xn ; yn) for n = (t + 1), (t + 2), ... .
This work considers both human-human (HH) and human-scene (HS) interactions for predictions. Since the HH model utilizes only historical coordinates for prediction and does not take into account for other objects/pedestrians, this lack of scene awareness is compensated through the HS interaction model (provided as an occupancy map) and the scene structure from the convolutional neural network. All three of these tasks are modeled separately and form a combined representation which is then passed through an LSTM decoder to generate the results.

Related Work

Some of the relevant works pertaining to Trajectory Prediction are discussed briefly below:

Semantic Segmentation: By labeling each pixel of an image with a corresponding class, we can augment other tasks that might require information pertaining to the subject’s environment. Previous works like SSeg-LSTM have found that for any Segmentation model, the features extracted from the encoder work just as well, if not better than the ones extracted from the model’s decoder. In this project, we verify this by comparing the performance of encoder and decoder features of Segmentation models like ResNeXt and DeepLab.

Scene understanding: A number of works have explored the effects of the environment on the trajectory of the subject. Kitani et al. used Inverse Reinforcement Learning to forecast human trajectory. Scene-LSTM divided the static scene into a Manhattan Grid and predicted the pedestrian’s location using LSTMs. We plan to train a sequential model that utilizes segmentation information from the scene to learn not only from the subject’s current trajectory but also its local environment.

Sequence modeling: Most recent works like Social-LSTM and Scene-LSTM have utilized LSTMs to model the subjects’ trajectories based on their social and environmental interactions. Recent works like TrajNet argue that Transformer Networks are more suitable for the task, thanks to their better capability to learn non-linear patterns. Since transformers work on the principle of attention, we experiment with combinations of GRU-based sequential models and attention mechanism to corroborate this.

Dataset

Figure 2. Example frames from the ETH dataset.

For this project, we use two of the most popular datasets on human trajectory prediction, namely the ETH and UCY datasets. These datasets contain videos with a fixed camera with a top-down view of a scene with pedestrians. ETH contains two subset video sequences (Hotel and Univ) while UCY has three sequences (Univ, Zara01, and Zara02). These sequences provide a myriad of pedestrian walking behaviors. In total, we collect 1050 samples, where each sample corresponds to a particular pedestrian whose features are of the shape 10x4, where 10 is the total number of frames associated with each pedestrian. Any pedestrian that appears in less then 10 associated frames is discarded. The last dimension comes comes from a set of (PedID, FrameID, X Y), where PedID is the Pedestrian ID, FrameID is the frame identification number, and X and Y corresponds to the normalized pixel coordinates of the pedestrian for a given frame.

Framework

Encoding Branches

Figure 2. Three main branches of the baseline framework.
Person

This submodule is used for encoding the spatial coordinates of the subject. A total of t(=5 frames {2 seconds}) time steps are observed by the model and predictions are made from t+1 until t+5. The number of input and output timesteps can be varied and these variations themselves can be treated as an ablation study. We first use a linear layer to encode each pair of coordinates into 64 features and pass it through a non linearity. These encoded features are then passed through a Gated Recurrent Unit (GRU) at every training time step. The final output of the GRU acts as our person features.

Social/ Group

Next, we look at the social interactions of the person of interest. This submodule aims to model the influence of presence of other pedestrians on the trajectory of the person of interest. This is done by constructing ocuupancy maps of the the surrounding of the pedestrian under consideration. We encode these interactions by dividing the immediate vicinity of the subject into a circular or log-circular grid. The influence of other people around the subject is measured as a function of the distance and relative angle between them. The ocupancy maps are are computed using: $$ O^{i}_t (a,b) = \Sigma_{(j \in N^{i})} \alpha_{ab}(x^{j}_{t}, y^{j}_{t}) $$ where \(\alpha_{ab}\) is a discrimination function of the radius that classifies whether the \(j^{th}\) pedestrian is inside the neighbourhood set \(N^{i}\) of the \(i^{th}\) pedestrian for (a,b) cell of the occupancy map. Similar to the person encoding, this is then passed through a GRU at every training step and the final output of the GRU is taken as the group features for the subject.

Scene Understanding

Finally, we encode the scene features of every sample. We hypothesize that given the short time span of our input sequence, taking only the last frame of a sequence so as to reduce the computational overhead is a viable tradeoff that provides the model with significant scene understanding. We do this by taking the last frame of the training sequence and passing it through the encoder of a pre-trained CNN model. This gives us global scene features for that particular timestep. These features are then repeated over the training steps and passed through a GRU to get the final scene features.

Incorporating Attention

Figure 3. The two attention mechanisms.

Although there have prior works which have explored incorporating attention for the the trajectory prediction task, these have been limited to either self attention models for the person's trajectory or attending the person's trajectory with the social interaction features. In this project, we propose a pair of alternating co-attention models where attention is used for both the social and scene features. To the extent of our knowledge combining all the three models and attention has not been explored in prior works.

Alternating Co-Attention

In this attention model introduced by Lu et al., We sequentially alternate between a combination of our encoding branch outputs and then combine them.We experiment with two attention mechanisms, namely, Scene attention and Person attention.

Scene attention is a co-attention mechanism where the person and group features attend to the image features, thus generating person-scene attention features and group-scene attention features. These attention features are then concatenated and passed througha linear layer before being input to the decoder.

Person attention, on the other hand, is a co-attention mechanism where the scene and group features attend to the person features, thus generating scene-person attention features and group-person attention features. Our intuition is to get the scene and group context for each time step of the subject's trajectory to aid the decoder's predictions. As before, the attention features are again conacatenated and passed through a linear layer before sent to the decoder.

The overall attention mechanism is formulated as follows: Given an attention operation defined as \( \hat{x} = A(X;g) \). Where \(X\) in the input which in the case of Person attention for a given sub-brach can be person encodings (or scene encodings) and person encodings (or group encodings) . with attention guidance derived from the secondary input i.e the if X is person encoding then guidance would be derived from the scene encodings and vice-versa. This attention operation outputs the attended vector, where the operations carried out are expressed in the following steps. $$H = tanh(W_x X + (W_g g) \mathbb{1}^T )$$ $$a^x = softmax(w^t_{hx}H)$$ $$\hat{x} = \Sigma(a_i^x x_i)$$ where \(\mathbb{1}\) is a vector with all elements to be 1. \(W_x, W_g \in R^{k×d} \)and \(w_{hx} \in R^k \) are parameters. \(a^x\) is the attention weight of feature \(X\). Similarly for scene attention \(X\) can either be person encodings (or scene encodings) and group encodings (or scene encodings) and we follow the same mechanism as stated for the person attention.

Decoder

Figure 4. Decoder architecture.

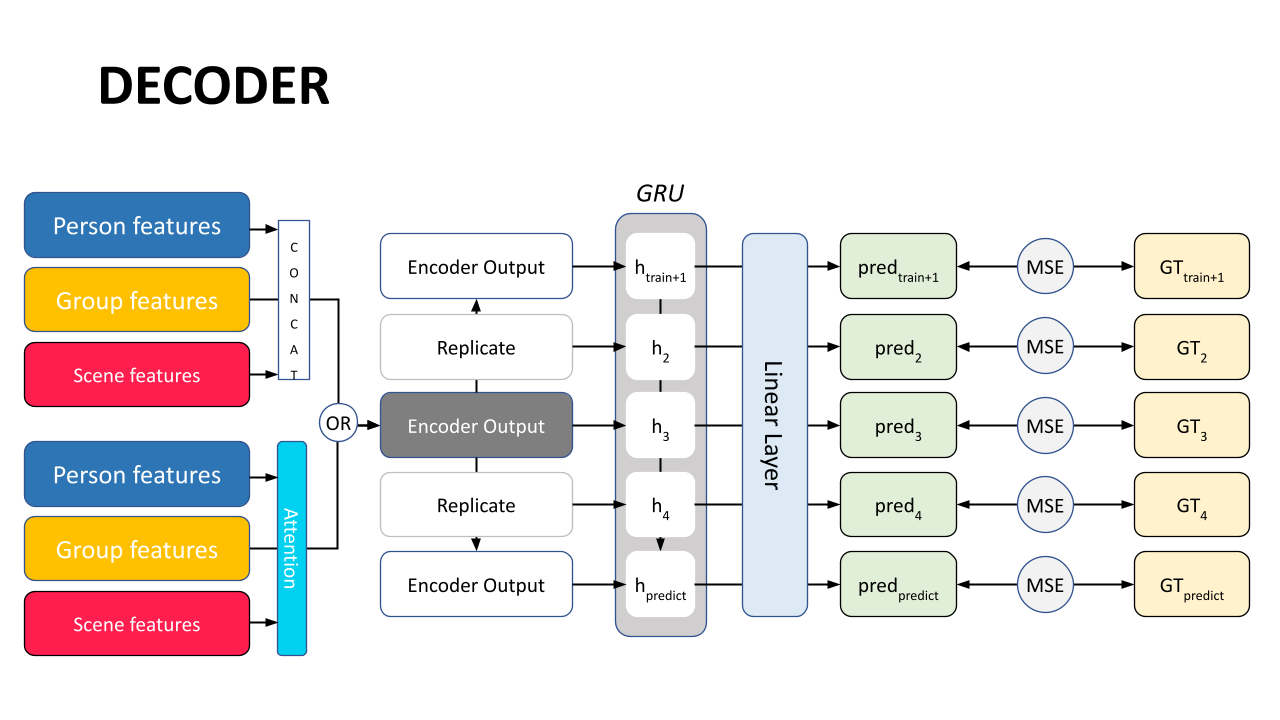
Finally, we bring it all together in the decoder. In the baseline, we simply sum the person, group, and scene features to get a non-sequential decoder input. We then replicate this input to resemble a 5 step sequence and pass it through a decoder GRU that gives us our prediction features at each step. These predictions features are passed through a linear layer to convert them into predicted coordinates and compared to the ground truth to calculate the Mean Squared Error.

In the attention model, we apply the attention mechanisms explained above on the person, group, and scene features. Then we use a simple MLP to encode the attention features from the different sub-branches as follows:

For Person attention model: $$ h^{scene} = tanh(W_{scene}(\hat{q}^{scene} + \hat{v}^{scene}))$$ $$ h^{group} = tanh(W_{group}[(\hat{q}^{group} + \hat{v}^{group}), h^{scene}])$$

For Scene attention model: $$ h^{person} = tanh(W_{person}(\hat{q}^{person} + \hat{v}^{person}))$$ $$ h^{group} = tanh(W_{group}[(\hat{q}^{group} + \hat{v}^{group}), h^{person}])$$

The attended features are then replicated to resemble a sequential input and treated to the same architecture explained above to get predicted coordinates.

Experiments and Results

In this section, we discuss the evaluation metrics and report the results of our different experiments evaluated on the ETH/UCY datasets. We also report results from an ablation study used to validate our choice of the scene feature encoder.

Metrics

For training, we use Mean Squared Error and we evaluate our models using Average Displacement Error (ADE) and Final Displacement Error (FDE), which are standard metrics in trajectory prediction tasks. ADE is the average of the Euclidian Distance between the predicted coordinates and the ground truth at every prediction step, whereas FDE is the Euclidian Distance between the final predicted coordinate and final ground truth target for a given sample.

$$ ADE = \frac{\Sigma_{i=1}^{N} \Sigma _{t = t_{observed+1}}^{t_{final}} \vert\vert Pred_t^i - GT_t^i\vert\vert_2}{ NT}$$ $$ FDE = \frac{\Sigma_{i=1}^{N} \vert\vert Pred_{t^i{_{final}}} - GT_{t^i{_{final}}}\vert\vert}{ N}$$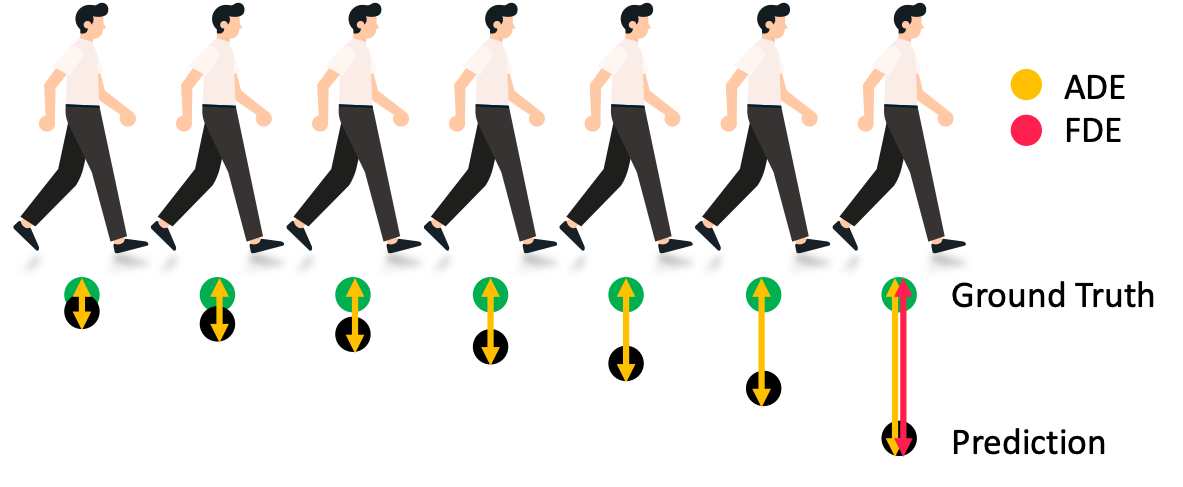
Figure 5. Visualizated example of the trajectory prediction metrics Average Displacement Error (ADE) and Final Displacement Error (FDE).

Experimental Setup

We conducted four experiments to explore the effects of changing the scene encoders, by excluding or adding attention mechanisms on person or group features, and using semantic segmentation information. In our experiments, we define the Baseline model by that proposed in Xue et al.. The particular component to notice is that of the encoder for scene features. In this model, the Convolutional Neural Network (CNN) is defined by three convolutional layers. For our experiments, we swap this scene encoder for a more complex CNN architecture, namely ResNeXt. It's important to clarify that while Syed et al refers to the scene features as "semantic segmentation information", and so do we for convention, the features produced by this submodule are CNN features not pixel-wise class prediction maps. In other words, these CNNs are just the encoder portion of an encoder-decoder semantic segmentation network. Syed et al does point out however, that these encoders area fine-tuned for the task of segmentation, so we follow these studies. However, to explore what would happen if we actually used pixel-wise predictions as scene features, we utilize a DeepLab model trained on CamVid to produce scene features. We then experiment with adding different attention mechanisms on either the person or group features. Further we also, explore the implications of taking feature maps from the decoder of a segmentation network.

Main Quantitative Results

Experimental Results
Model FDE ADE
Baseline 0.142 0.081
ResNeXt Encoder + Person Attention 0.124 0.077
ResNeXt Encoder + Scene Attention 0.144 0.086
DeepLabV3 Decoder + Person Attention 0.15 0.079

In the table above, we compute the Average Displacement Error (ADE) and Final Displacement Error (FDE) and compare for different models using distinct scene information extraction and attention mechanisms. Our results show that swapping the feature encoder with ResNeXt and adding attention on the person features significantly reduced the ADE and FDE when compared to the baseline. Interestingly, adding attention on the group features achieved comparatively similar ADE and FDE when compared to the baseline, but not any lower. Additionally, we attempted to use actual semantic segmentation predictions as our scene features, outperforming the baseline in ADE but not FDE, thus showing an improvement.


Main Qualitative Results

CNN Ablation Study

For this project, we were interested in improving the extraction of segmentation information from a scene. As a result, when studying the baseline which consisted of a CNN architecture of three convolutional layers (with maxpool and batch norm layers), we proposed that swapping this encoder with more complex, pre-trained CNN architectures could provide better scene feature extraction. In this ablation study, we compare three different popular CNN models: VGG-16, ResNet-18, and ResNeXt-50. Since we wish to compare the scene feature extraction capabilities of these pre-trained models, we utilize a SegNet decoder to achieve the segmentation results. While the segmentation decoder could be any other semantic segmentation decoder (e.g. U-Net, DeepLab), we utilize SegNet per the studies by Syed et al.

Experimental Results
CNN Architecture Segmentation Decoder Head mIoU
VGG-16 SegNet 87.7
ResNet-18 SegNet 89.3
ResNeXt-50 SegNet 91.3

In the table above, we show the results from the ablation study to choose a new encoder for the Trajectory Prediction model. For this study, we utilize three CNN architectures pre-trained on ImageNet. In Syed et al, VGG-16 is selected as the feature extractor for the scene features. Syed et al argues that a CNN encoder trained for the task of semantic segmentation can provide better scene features for pedestrian trajectory predictions. Thus, we train and evaluate each model presented above on the CamVid dataset. Then, we evaluate the performance of each model by using the mean Intersection over Union (mIoU) score, which is the average IoU score of all classes. As shown, the segmentation model with a ResNeXt encoder achieves the greatest mIoU score. Therefore, we select ResNeXt as our encoder of choice for the main experiments.

Video Presentation